ĀŪ(l®Ęi)‘ī£ļĺW(w®£ng)Ĺj(lu®į)ŔY‘ī ◊ų’Ŗ£ļ÷–ŅľĺW(w®£ng)’ŻņŪ 2019-08-31 17:43:36
°°°°Őō ‚Ķń∆Ĺ––ňńŖÖ–őľįĶ»—ŁŐ›–ő ĹňńŖÖ–őĶń÷ų“™É»(n®®i)»›£¨ňŁāÉĶńĎ™(y®©ng)”√∑«≥£ŹV∑ļ°£¨F(xi®§n)ĺÕňŁāÉĶń◊R(sh®™)ĄeólľĢŇeņż’f(shu®≠)√ų£¨Ļ©Õ¨ĆW(xu®¶)āÉÖĘŅľ°£
°°°°“Ľ°Ę∆Ĺ––ňńŖÖ–ő
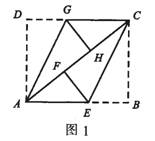
°°°°ņż1 »ÁąD1£¨”–“Ľĺō–őľą∆¨ABCD£¨∑≠’Ř∠B°Ę∠D£¨ ĻBC°ĘAD«°ļ√¬š‘ŕAC…Ō°£‘O(sh®®)F°ĘH∑÷Ąe «B°ĘD¬š‘ŕAC…ŌĶńŁc(di®£n)£¨E°ĘG∑÷Ąe «’ŘļŘCE°ĘAGŇcAB°ĘCDĶńĹĽŁc(di®£n)°£«ů◊C£ļňńŖÖ–őAECG «∆Ĺ––ňńŖÖ–ő°£
°°°°’ĄŐō ‚ňńŖÖ–őĶń◊R(sh®™)Ąe
°°°°∑÷őŲ£ļ“™◊C√ųňńŖÖ–őAECG «∆Ĺ––ňńŖÖ–ő£¨Ó}÷–“—”–ólľĢCG°őAE£¨“ÚīňŅ…ŅľĎ]◊C√ųCG=AE£¨ņŻ”√““ĽĹMƶ(du®¨)ŖÖ∆Ĺ––«“ŌŗĶ»ĶńňńŖÖ–ő «∆Ĺ––ňńŖÖ–ő”£Ľ“≤Ņ…“‘ŅľĎ]◊C√ųAG°őCE£¨ņŻ”√“É…ĹMƶ(du®¨)ŖÖ∑÷Ąe∆Ĺ––ĶńňńŖÖ–ő «∆Ĺ––ňńŖÖ–ő”°£Ō¬√ś”√Ķŕ∂Ģ∑Nňľ¬∑◊C√ų°£
°°°°◊C√ų£ļ‘ŕĺō–őABCD÷–£¨“Ú?y®§n)ťAD°őBC£¨ňý“‘∠DAC=∠BCA°£”…Ó}“‚£¨Ķ√∠GAH=
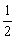
∠DAC£¨∠ECF=
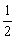
∠BCA£¨ňý“‘∠GAH=∠ECF£¨ňý“‘AG°őCE °£”÷“Ú?y®§n)ťCG°őAE£¨ňý“‘ňńŖÖ–őAECG «∆Ĺ––ňńŖÖ–ő°£
°°°°Łc(di®£n)‘u(p®™ng)£ļ∆Ĺ––ňńŖÖ–ő≥£“äĶńŇ–∂®∑Ĺ∑®ŖÄ”–£ļĘŔÉ…ĹMƶ(du®¨)ŖÖ∑÷ĄeŌŗĶ»ĶńňńŖÖ–ő£ĽĘŕƶ(du®¨)Ĺ«ĺÄĽ•Ōŗ∆Ĺ∑÷ĶńňńŖÖ–ő£ĽĘŘÉ…ĹMƶ(du®¨)Ĺ«∑÷ĄeŌŗĶ»ĶńňńŖÖ–ő°£Ŗ\(y®īn)”√ēr(sh®™)£¨“™ž`ĽÓŖxďŮ°£»ÁĻŻ“Ľ∑N∑Ĺ∑®≤Ľ“◊Ĺ‚≥Ų£¨Ņ…“‘áL‘á∆šňŻĶń∑Ĺ∑®°£
°°°°∂Ģ°Ęĺō–ő
°°°°ņż2 »ÁąD2£¨‘ŕ°ųABC÷–£¨AB=AC°£AD⊥BC£¨īĻ◊„읣c(di®£n)D°£AN «°ųABCÕ‚Ĺ«∠CAMĶń∆Ĺ∑÷ĺÄ£¨CE⊥AN£¨īĻ◊„읣c(di®£n)E°£«ů◊C£ļňńŖÖ–őADCEěťĺō–ő°£
°°°°’ĄŐō ‚ňńŖÖ–őĶń◊R(sh®™)Ąe
°°°°∑÷őŲ£ļ“™◊C√ųňńŖÖ–őADCRěťĺō–ő£¨Ó}‘O(sh®®)÷–“—”–É…āÄ(g®®)Ĺ« «÷ĪĹ«ĶńólľĢ£¨Ņ…ŅľĎ]ņŻ”√“”–»żāÄ(g®®)Ĺ« «÷ĪĹ«ĶńňńŖÖ–ő «ĺō–ő”ĀŪ(l®Ęi)◊C√ų£¨Ļ ÷Ľ“™◊C√ų∠DAE «÷ĪĹ«ľīŅ…°£
°°°°◊C√ų£ļ‘ŕ°ųABC÷–£¨AB=AC£¨AD⊥BC£¨ňý“‘∠BAD=∠DAC°£“Ú?y®§n)ťAN «°ųABCÕ‚Ĺ«∠CAMĶń∆Ĺ∑÷ĺÄ£¨ňý“‘∠MAE=∠CAE°£Ļ ∠DAE=∠DAC+∠CAE=°£

”÷“Ú?y®§n)ťAD⊥BC£¨CE⊥AN£¨ňý“‘ňńŖÖ–őADCEěťĺō–ő°£
°°°°Łc(di®£n)‘u(p®™ng)£ļĺō–ő≥£“äĶńŇ–∂®∑Ĺ∑®”–£ļĘŔ»żāÄ(g®®)Ĺ« «÷ĪĹ«ĶńňńŖÖ–ő£ĽĘŕ”–“ĽāÄ(g®®)Ĺ« «÷ĪĹ«Ķń∆Ĺ––ňńŖÖ–ő£ĽĘŘÉ…ólƶ(du®¨)Ĺ«ĺÄŌŗĶ»Ķń∆Ĺ––ňńŖÖ–ő°£
°°°°»ż°ĘŃ‚–ő
°°°°ņż3 »ÁąD3£¨‘ŕŐ›–őľą∆¨ABCD÷–£¨AD°őBC£¨AD£ĺCD°£ĆĘľą∆¨—ōŖ^(gu®į)Łc(di®£n)DĶń÷ĪĺÄ’ŘĮB£¨ ĻŁc(di®£n)C¬š‘ŕAD…ŌĶńŁc(di®£n)C1Ő飨’ŘļŘDEĹĽBC”ŕŁc(di®£n)E°£«ů◊C£ļňńŖÖ–őCDC1E «Ń‚–ő°£
°°°°’ĄŐō ‚ňńŖÖ–őĶń◊R(sh®™)Ąe
°°°°∑÷őŲ£ļ”…”ŕ «’ŘĮBÜĖ(w®®n)Ó}£¨“Úīň”–ļ‹∂ŗŖÖŌŗĶ»°ĘĹ«ŌŗĶ»£¨Ņ…“‘ŅľĎ]ņŻ”√“ňńólŖÖ∂ľŌŗĶ»ĶńňńŖÖ–ő «Ń‚–ő”ĀŪ(l®Ęi)◊C√ų°£
°°°°◊C√ų£ļ”…Ó}“‚Ņ…÷™°ųCDE°’°ųC1DE£¨Ąt”–CD=C1D£¨∠C1DE=∠CDE£¨CE=C1E°£“Ú?y®§n)ťAD°őBC£¨ňý“‘∠C1DE=∠CED°£Ļ ∠CDE=∠CED£¨”ŕ «CD=CE°£ňý“‘CD=C1D=C1E=CE£¨ňńŖÖ–őCDC1E «Ń‚–ő°£
°°°°Łc(di®£n)‘u(p®™ng)£ļŃ‚–ő≥£“äĶńŇ–∂®∑Ĺ∑®”–£ļĘŔňńólŖÖ∂ľŌŗĶ»ĶńňńŖÖ–ő£ĽĘŕ”–“ĽĹMŗŹŖÖŌŗĶ»Ķń∆Ĺ––ňńŖÖ–ő£ĽĘŘƶ(du®¨)Ĺ«ĺÄĽ•ŌŗīĻ÷ĪĶń∆Ĺ––ňńŖÖ–ő°£‘ŕ’ŘĮBÜĖ(w®®n)Ó}÷–£¨»ÁĻŻ”–∆Ĺ––ĺÄĶńólľĢ£¨“Ľį„∂ľēĢ(hu®¨)”–Ķ»—Ł»żĹ«–őīś‘ŕ°£Ŗ@Łc(di®£n)Ď™(y®©ng)ģĒ(d®°ng)÷ō“ē°£
°°°°ňń°Ę’ż∑Ĺ–ő
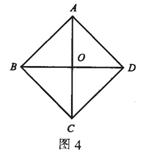
°°°°ņż4 »ÁąD4ňý ĺ£¨‘ŕňńŖÖ–őABCD÷–£¨AB=BC=CD=DA£¨Ć¶(du®¨)Ĺ«ĺÄACŇcBDŌŗĹĽ”ŕŁc(di®£n)O°£»Ű≤Ľ‘Ųľ”»őļő◊÷ńłŇc›o÷ķĺÄ£¨“™ ĻňńŖÖ–őABCD «’ż∑Ĺ–ő£¨ĄtŖÄ–Ť‘Ųľ”Ķń“ĽāÄ(g®®)ólľĢ « °£
°°°°’ĄŐō ‚ňńŖÖ–őĶń◊R(sh®™)Ąe
°°°°∑÷őŲ£ļŖ@ «“ĽĶņť_∑Ň–ÕÓ}ńŅ°£łýďĢ(j®ī)“—÷™ólľĢ÷™ňńŖÖ–őABCD «Ń‚–ő£¨“™ ĻňńŖÖ–őABCD «’ż∑Ĺ–ő£¨įī∆šŇ–∂®∑Ĺ∑®÷Ľ“™‘Ųľ”ólľĢ∠BAD=90°£¨ĽÚ∠ABD=45°£¨ĽÚAC=BDĶ»°£
°°°°Ĺ‚£ļ¬‘°£
°°°°Łc(di®£n)‘u(p®™ng)£ļ’ż∑Ĺ–ő≥£“äĶńŇ–∂®∑Ĺ∑®”–£ļĘŔ”–“ĽĹMŗŹŖÖŌŗĶ»Ķńĺō–ő£ĽĘŕ”–“ĽāÄ(g®®)Ĺ« «÷ĪĹ«Ķń£®ĽÚ?q®Ī)¶Ĺ«ĺÄŌŗĶ»Ķń£©Ń‚–ő°£
°°°°őŚ°ĘĶ»—ŁŐ›–ő
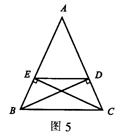
°°°°ņż5 »ÁąD5£¨‘ŕĶ»—Ł°ųABC÷–£¨AB=AC°£BD⊥AC£¨CE⊥AB£¨īĻ◊„∑÷Ąe읣c(di®£n)D°ĘE£¨ŖBĹ”DE°£«ů◊C£ļňńŖÖ–őBCDE «Ķ»—ŁŐ›–ő°£
°°°°’ĄŐō ‚ňńŖÖ–őĶń◊R(sh®™)Ąe
°°°°∑÷őŲ£ļ“™◊C√ųňńŖÖ–őBCDE «Ķ»—ŁŐ›–ő£¨ ◊Ō»“™◊C√ųňŁ «Ő›–ő£¨‘Ŕ◊C√ų∆šÉ…—ŁŌŗĶ»ľīŅ…°£”…ąD–ő÷™BEŇcCDÔ@»Ľ≤Ľ∆Ĺ––£¨“Úīň“™◊C√ųDE°őBC£¨Ņ…Õ®Ŗ^(gu®į)“Õ¨őĽĹ«ŌŗĶ»£¨É…÷ĪĺÄ∆Ĺ––”ĀŪ(l®Ęi)Ĺ‚õQ°£“™◊C√ųŖ@āÄ(g®®)Ő›–ő «Ķ»—ŁŐ›–ő£¨Ņ…Õ®Ŗ^(gu®į)’f(shu®≠)√ųÉ…—ŁŌŗĶ»Ķń∑Ĺ∑®Ŗ_(d®Ę)ĶĹ°£
°°°°◊C√ų£ļ‘ŕĶ»—Ł°ųABC÷–£¨AB=AC£¨∠ABC=∠ACB°£“Ú?y®§n)ťBD⊥AC£¨CE⊥AB£¨ňý“‘∠BEC=∠CDB=90°°£”÷BC=CB£¨ňý“‘°ųBEC°’°ųCDB£®AAS£©°£”ŕ «BE=CD°£Źń∂ÝAB-BE=AC-CD£¨ľīAE=AD°£ňý“‘∠AED=∠ADE°£ňý“‘∠ABC=∠AED=
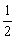
£®180°-∠A£©°£ňý“‘DE°őBC°£∂ÝBEŇcCD≤Ľ∆Ĺ––£¨ňý“‘ňńŖÖ–őBCDE «Ő›–ő°£”÷“Ú?y®§n)ťBE=CD£¨Ļ ňńŖÖ–őBCDE «Ķ»—ŁŐ›–ő°£
°°°°Łc(di®£n)‘u(p®™ng)£ļĶ»—ŁŐ›–ő≥£“äĶńŇ–∂®∑Ĺ∑®”–£ļĘŔÉ…—ŁŌŗĶ»ĶńŐ›–ő£ĽĘŕÕ¨“ĽĶ◊…ŌĶńÉ…āÄ(g®®)Ĺ«ŌŗĶ»ĶńŐ›–ő£ĽĘŘƶ(du®¨)Ĺ«ĺÄŌŗĶ»ĶńŐ›–ő°£
–¬≥ű»żŅžíŖīaÍP(gu®°n)◊Ę
÷–ŅľĺW(w®£ng)őĘ–ŇĻęĪäŐĖ(h®§o)
√Ņ»’Õ∆ňÕĆW(xu®¶)Ńē(x®™)ľľ«…£¨ĆW(xu®¶)Ņ∆÷™◊R(sh®™)Łc(di®£n)
÷ķń„”≠Ĺ”2020ńÍ÷–Ņľ£°
°°°° ög”≠ Ļ”√ ÷ôC(j®©)°Ę∆ĹįŚĶ»“∆Ą”(d®įng)‘O(sh®®)āš‘LÜĖ(w®®n)÷–ŅľĺW(w®£ng)£¨2025÷–Ņľ“Ľ¬∑Ň„įťÕ¨––£°>>Łc(di®£n)ďŰ≤ťŅī
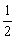 ∠DAC£¨∠ECF=
∠DAC£¨∠ECF=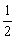 ∠BCA£¨ňý“‘∠GAH=∠ECF£¨ňý“‘AG°őCE °£”÷“Ú?y®§n)ťCG°őAE£¨ňý“‘ňńŖÖ–őAECG «∆Ĺ––ňńŖÖ–ő°£
∠BCA£¨ňý“‘∠GAH=∠ECF£¨ňý“‘AG°őCE °£”÷“Ú?y®§n)ťCG°őAE£¨ňý“‘ňńŖÖ–őAECG «∆Ĺ––ňńŖÖ–ő°£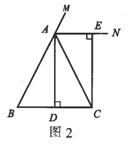
 ”÷“Ú?y®§n)ťAD⊥BC£¨CE⊥AN£¨ňý“‘ňńŖÖ–őADCEěťĺō–ő°£
”÷“Ú?y®§n)ťAD⊥BC£¨CE⊥AN£¨ňý“‘ňńŖÖ–őADCEěťĺō–ő°£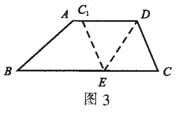
 £®180°-∠A£©°£ňý“‘DE°őBC°£∂ÝBEŇcCD≤Ľ∆Ĺ––£¨ňý“‘ňńŖÖ–őBCDE «Ő›–ő°£”÷“Ú?y®§n)ťBE=CD£¨Ļ ňńŖÖ–őBCDE «Ķ»—ŁŐ›–ő°£
£®180°-∠A£©°£ňý“‘DE°őBC°£∂ÝBEŇcCD≤Ľ∆Ĺ––£¨ňý“‘ňńŖÖ–őBCDE «Ő›–ő°£”÷“Ú?y®§n)ťBE=CD£¨Ļ ňńŖÖ–őBCDE «Ķ»—ŁŐ›–ő°£